Here are some ideas on a new technique for solving math problems using mind maps.
What is mind mapping?
Mind mapping is a special form of note-taking. Here are some essential features:
- You take a (preferably large) sheet of paper in landscape format.
- You write the topic / the problem in the middle of the sheet and draw a frame around it.
- You write the main aspects and main ideas around that central topic and link them through lines to the center.
- You expand the ideas in these “main branches” into subbranches etc.
- Wherever appropriate, you should use figures, colours, arrows to link branches etc.
Here are three examples from Wikipedia. Beware: I didn’t bother to check their content. I’m just interested in their different layout and appearance.
A handdrawn map:

A simpler handdrawn map:

A computer map:
How can mind maps be used for solving problems?
Let’s start with two principal uses:
- Using mind maps to examine a given problem.
- Using mind maps to organize problem solving tools.
These two uses may even be combined, leading to the use of two mindmaps at a time:
- a “problem map” for dealing with the problem itself and
- a “tool map” (or several of them) containing problem solving tools – from general ones (e.g. the ones presented in Polya’s “How to Solve It”) to highly specialized ones (e.g. for dealing with Poisson processes).
Problem Maps
The key difficulty in using mind mapping for mathematical problem solving is to combine conventional mind map layout with ordinary (and often lengthy) computations, because the latter simply don’t fit well into the mind map layout.
After some experiments, I have found a way that works fine for me (and which can certainly be modified in a number of ways):
- I use the upper third of the sheet for the problem map.
- The two lower thirds are tiled in boxes and are used for computations and working out details.
- The middle line is a simple convenience. (See the example below.)
The result is a hybrid form of notetaking, combining mind maps and more conventional notes.
The computations and details can be referenced in the problem map by numbers, if necessary.
In this way, I can use the problem map for collecting ideas and for directing and “supervising” the detail work.
The use of boxes was inspired by an article “Stop Making Stupid Mistakes” by R. Rusczyk on www.artofproblemsolving.com.
It should be clear that problem maps are intended for finding a solution, not presenting one.
An Example
Here comes a sample problem map. The problem is very easy, but the sample should show the flavour of the method. The map deals with the following problem:
Show that there are infinitely many positive integers which are not the sum of a square and a prime. (This exercise is taken from Arthur Engel’s book “Problem-Solving Strategies” (p. 133, no. 63 a).)
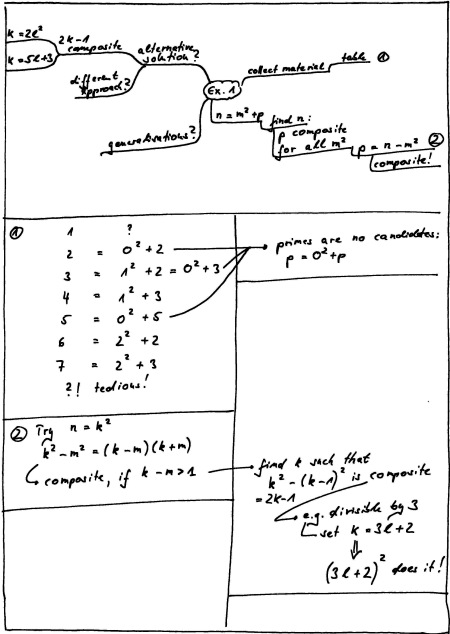
Advantages of the hybrid layout
- Due to the map’s layout, it’s easy to collect ideas and group them. Further ideas can later be added at appropriate places in the map.
- The problem map helps you not to lose sight of the overall picture.
- If you are stuck, the problem map can help you to bring structure into your thoughts.
- It’s easy to keep track of several aspects or approaches, of aims and sub-aims etc.
- Using words, mathematical terms and figures in the problem map and in the boxes allows you to exploit the advantages of each of these three representations.
- The ideas and chains of thought documented in the problem map and the boxes can be scrutinized.
- Mind mapping itself is easy to learn and fun to use.
Some ideas on possible variations
- Use larger sheets for more complex problems (A3 instead of A4).
- Use separate sheets for problem map and conventional math notes.
- Begin with conventional math notes and start the problem map as soon as you run into difficulties.
- Change details of layout (e.g. use more space for the problem map, place the theme of your problem map at the left margin rather than at the center …)
- If reasonable, use auxiliary mind maps in the boxes.
Tool Maps
The basic idea in using tool maps is to collect and structure problem solving tools in mind maps.
The tool maps can be organized along several concepts, like:
Stages of problem solving, e.g. Polya’s scheme from “How to Solve It”:
- “understanding the problem”
- “devising a plan”
- “carrying out the plan”
- “looking back”.
Standard situations in problem solving, e.g.
- “looking for new approaches”
- “overcoming frustration”
- “need for information”
- “my most frequent errors in problem solving”.
Mathematical objects involved, e.g.
- matrices,
- polynomes or
- inequalities.
Here comes a small collection of tool maps [more…]
A brief discussion of Tool Maps
We start with its advantages:
- Most important: In constructing and improving your own tool maps, you learn a lot about problem solving and especially your personal problem solving behaviour.
- Tools maps act as reminders for techniques you might otherwise have overlooked.
- Tool maps can help novices with adopting new working heuristics.
- Tool maps are very flexible and can be adapted to all sorts of experience, needs and special fields.
- Due to their graphical representation and their structure, tool maps are easier to scan and to expand than conventional catalogues or lists.
- Tool maps may help to share problem solving techniques in a group by making “implicit” problem solving techniques “explicit”.
Here are some disadvantages:
- Sometimes tool maps may become messy and overloaded and need redrawing.
- To use tool maps consistently, it’s essential that the tool maps are easily accessible, (e.g. as a poster at the working place, or as a handy folder).
When to use Tool Maps
The tool maps can be of use especially in the following situations:
- You are stuck and need some new ideas:
Consult the tool maps and look for new approaches. - You are a novice and want to learn some new problem solving techniques:
Use tool maps as a kind of “recipe book”. - You want to make sure that you do not overlook some important aspects in dealing with your problem:
Use tool maps as checklists.
It is expressly NOT suggested to use the tool maps in every stage of problem solving.
How to combine Problem Maps and Tool Maps
Problem maps and tool maps are two modules that can be used separately.
However, using them in combination may lead to a number of interesting problem solving practices.
Here are some ideas.
For me, the following process works well:
- I start with collecting seminal ideas in the problem map. At this initial stage, I make use of the tool maps.
- Intuitively I chose the most promising approach and work out the details in the boxes.
Usually, this involves looking at special or extreme cases or drawing a picture or finding another appropriate representation of the problem. - If none of the ideas collected before leads to a solution, I use the tool maps again and look for further approaches. I can now use the information I have collected up to this
time. - I describe and analyze obstacles in the problem map and try to develop new approaches using this information.
- When finishing work on a problem, I ask myself why or why not I have found a solution and what steps were crucial.
If necessary, I add new tools to the tool maps.
Although the process of using problem maps may seem rather formal, there is much room for intuition and gut feeling.
Reblogged this on RJ-11 Amazing Techno Futures.